Proving natural numbers are infinity in Coq

Introduction

An interesting fact about math is that you can demonstrate things. A lot of people thinks that demonstrate is exemplify something, but it is not. It’s common to see people saying that $1 + 1 = 2$, just like one apple plus one apple is two apples. But, this is not a demonstration. A demonstration is a logical proof that something is true, by a formal way. You cannot say that every 1 plus itself is equal to two. Boolean algebra is a good example of this. In Boolean algebra, $1 + 1 = 1$. So, you can’t say that aways $1 + 1 = 2$.

What is Coq?

Coq is a software that allows you to write proofs. It is a proof assistant based on the calculus of inductive constructions. It is a functional programming language based on lambda calculus. I won’t talk about lambda calculus and the calculus of inductive constructions, but you can find more information about them on Wikipedia.

What is a formal proof?

A formal proof is a process based on logical rules and axioms used to demonstrate some theorem. The goal is to show an absolute truth that some affirmation is faithful by following strict rules.

The proof

A simple way to prove that natural numbers are infinite is by defining that given a natural number ($n: nat$), $n + 1$ will return natural numbers greater than $n$.

You need to make it because this theorem proves that natural numbers are infinite by showing that given any natural numbers, you can always find a natural number greater than it, by summing $1$ to it.

So, lets to define our theorem in Coq:

Theorem plus_1_natural : forall n : nat, 1 + n = S n /\ S n > n.

The forall keyword means the theorem is valid for all natural numbers. The $\land$ means the theorem is a conjunction, and the $S$ is the successor function. So, the theorem says that given a natural number $n$, $1 + n$ is equal to $S n$, and $S n$ is greater than $n$.

Lets to prove the theorem:

Proof.
  intros n.
  split.
  - reflexivity.
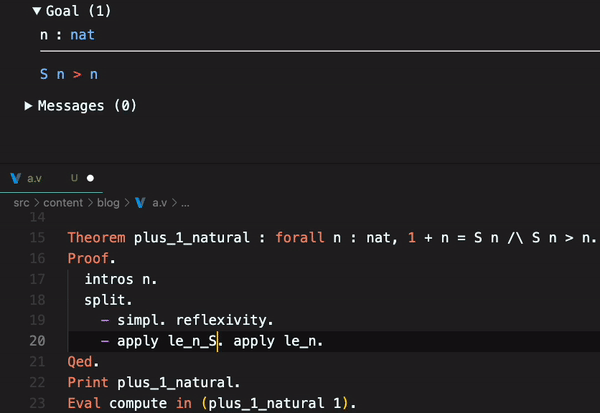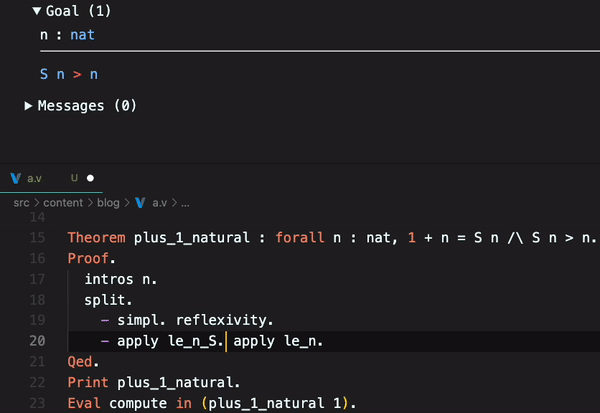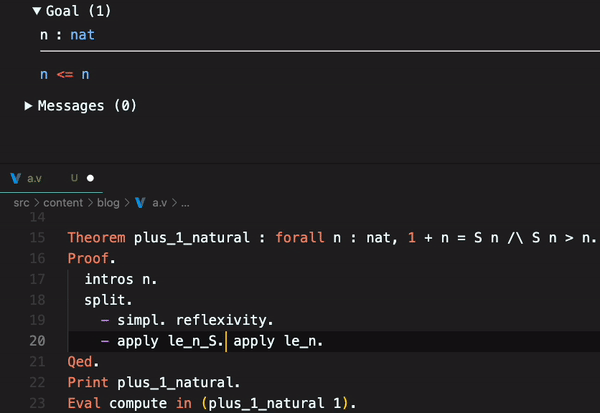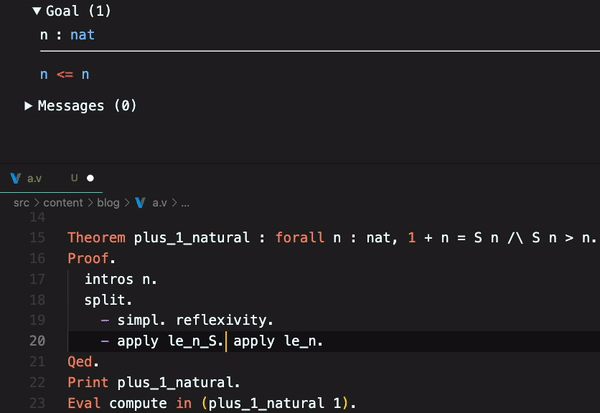
  - apply le_n_S. apply le_n.
Qed.

intros n introduces the universal quantifier forall and the arbitrary natural number $n$ as a variable. The split. splits the objective into two subgoals. One for each conjunct $\land$. The hyphen is to refer to the subgoal. The reflexivity. is to prove that something equals to itself. Like $1 + n = S n$, because $1 + n$ is equal to $S n$. You can reduce it, like:

• $1 + 1 = 2$.
• $2 = 2$.

Coq have some macros that abstracts some proofs. We can see this reducing using simpl.:

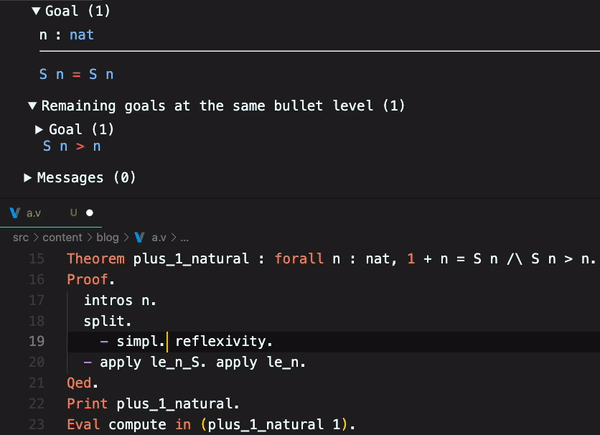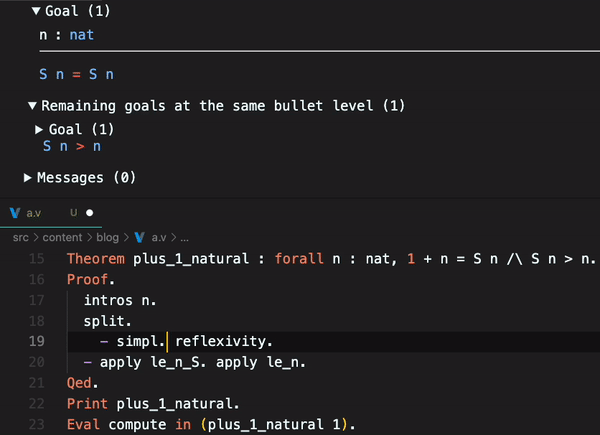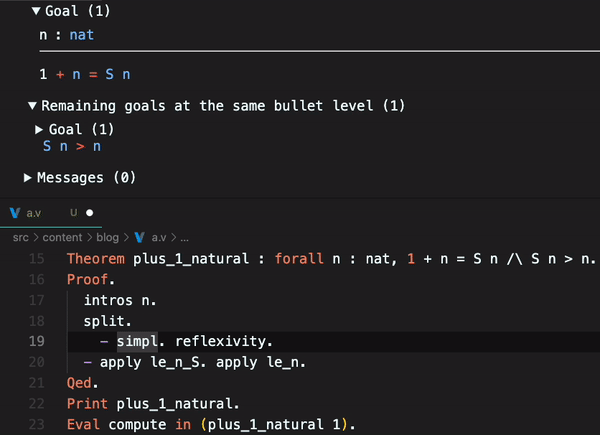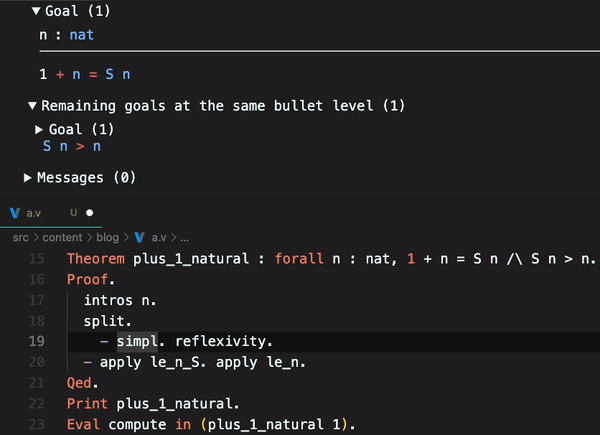
Coq gives us some theorems related to natural numbers ordering, like le_n_S and le_n. These theorems can be used to reduce steps of our proof, replacing them with the applied theorem. In math, the le it is $\leq$, less than or equal.

• le_n any natural number is less than or equal to itself. $n \leq n$ is a true statement for any natural number $n$.

• le_n_S says that if $n \leq m$, then $S n \leq S m$. So, if $n \leq n$, then $S n \leq S n$.

The apply le_n_S. definition is le_n_S : forall n m : nat, n <= m -> S n <= S m, and le_n that le_n : forall n : nat, n <= n. So, to read the apply le_n_S. apply le_n. is: “Given a natural number n, if n <= n, then S n <= S n”. And this is true, because n <= n is true, and S n <= S n is true too. So, the theorem is proved. Qed. means that the proof is finished.

You can also see it on CoqIDE:

Conclusion

You can also show the output of the proof and run the proof. So, lets do it.

You can use Print to show the definition of some theorem, and Eval compute in to run the proof. In the end, our proof will be:

Theorem plus_1_natural : forall n : nat, 1 + n = S n /\ S n > n.
Proof.
  intros n.
  split.
  - reflexivity.
  - apply le_n_S. apply le_n.
Qed.
Print plus_1_natural.
Eval compute in (plus_1_natural 1).

And the output will be:

plus_1_natural = fun n : nat => conj eq_refl (le_n_S n n (le_n n))
: forall n : nat, 1 + n = S n /\ S n > n

= plus_1_natural 1
: 1 + 1 = 2 /\ 2 > 1